Throughout history, the Pythagorean theorem has stood as a cornerstone of geometry, providing a critical foundation for countless mathematical applications. Recently, a groundbreaking new Pythagorean proof has emerged, challenging the conventional understanding and offering fresh insights into this age-old principle. This novel proof not only expands our comprehension of geometric relationships but also reflects the dynamic nature of mathematical discovery and progress. As we delve into this innovative proof, we will explore the implications it holds for both academia and practical applications, shedding light on its potential to reshape the landscape of mathematics.
Mathematics has long been a field characterized by exploration and the relentless pursuit of knowledge. The introduction of a new Pythagorean proof exemplifies this pursuit, as it represents a pivotal moment in the ongoing quest to understand the fundamental truths of the universe. This proof, while rooted in the familiar principles of the Pythagorean theorem, offers a fresh perspective that invites scholars and enthusiasts alike to reconsider traditional methodologies and concepts. In doing so, it underscores the importance of innovation and the continuous evolution of mathematical thought.
The broader implications of this new proof extend beyond the realm of mathematics, touching upon various scientific disciplines and technological advancements. By enhancing our understanding of geometric properties, this proof holds the potential to influence fields such as physics, engineering, and computer science, among others. As we embark on a comprehensive exploration of this new Pythagorean proof, we will uncover its origins, examine its derivation, and consider the myriad ways it may impact both theoretical and applied sciences.
Table of Contents
- The Origins of the Pythagorean Theorem
- Traditional Proofs: A Historical Perspective
- The Emergence of the New Pythagorean Proof
- Methodology Behind the New Proof
- Implications for Modern Mathematics
- Applications in Science and Technology
- Comparison with Traditional Proofs
- Educational Impact and Opportunities
- Theoretical Implications and Future Research
- Criticism and Controversies
- Support from the Mathematical Community
- Future Directions and Innovations
- Mathematical Philosophy and the New Proof
- Global Perspectives on the New Proof
- Conclusion
- FAQs
The Origins of the Pythagorean Theorem
The Pythagorean theorem, named after the ancient Greek mathematician Pythagoras, is one of the most renowned and widely used theorems in mathematics. It establishes a fundamental relationship between the sides of a right-angled triangle, stating that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This theorem has been a central element in geometry, forming the basis for many mathematical advancements and applications.
Pythagoras, who lived around 570–495 BC, is credited with the formalization of this theorem, although evidence suggests that variants of this relationship were known to ancient civilizations long before his time. Notably, the Babylonians and Indians had recognized similar geometric principles, as evidenced by their cuneiform tablets and Vedic texts, respectively. The Pythagorean theorem was thus an integral part of ancient mathematical knowledge, symbolizing the universality and timelessness of mathematical truths.
The historical significance of the Pythagorean theorem cannot be overstated. It has been pivotal in the development of various mathematical disciplines, including algebra, trigonometry, and calculus. Its simplicity and elegance have made it a fundamental concept taught in educational institutions worldwide, serving as an entry point for students to explore more complex mathematical ideas.
Traditional Proofs: A Historical Perspective
The Pythagorean theorem has been proven in numerous ways over the centuries, with each proof offering a unique perspective on this geometric relationship. Traditional proofs have ranged from algebraic approaches to geometric dissections, each contributing to the rich tapestry of mathematical knowledge. Among the most famous traditional proofs is Euclid's geometric proof, which relies on the construction of squares on the sides of a triangle to demonstrate the theorem's validity.
Another notable proof is attributed to the ancient Indian mathematician Bhaskara, who provided an elegant visual demonstration using a single diagram. This approach, often referred to as the "Behold" proof, showcases the theorem's validity through a straightforward yet powerful visual representation. Bhaskara's proof exemplifies the creative and diverse methods mathematicians have employed to explore the Pythagorean theorem.
Over time, mathematicians from various cultures and eras have contributed to the development of traditional proofs, each adding a layer of depth and understanding to this fundamental theorem. These proofs not only highlight the universality of mathematical principles but also underscore the collaborative nature of mathematical discovery, as scholars build upon the work of their predecessors to expand the boundaries of human knowledge.
The Emergence of the New Pythagorean Proof
The advent of the new Pythagorean proof marks a significant milestone in the ongoing exploration of mathematical principles. This innovative proof, developed by a team of contemporary mathematicians, offers a fresh perspective on the relationship between the sides of a right-angled triangle. By challenging traditional methodologies, this proof invites a reevaluation of established concepts and encourages further exploration of geometric relationships.
The development of the new proof was driven by a desire to uncover novel insights and expand the scope of mathematical understanding. Through rigorous research and creative problem-solving, the team succeeded in deriving a proof that not only adheres to the principles of the Pythagorean theorem but also introduces new elements that enhance its complexity and depth.
This groundbreaking proof has garnered attention from the mathematical community, sparking discussions and debates about its implications and potential applications. As scholars continue to analyze and validate the new proof, it is poised to become an integral part of the mathematical canon, inspiring future generations of mathematicians to explore the ever-evolving landscape of geometric theory.
Methodology Behind the New Proof
The methodology employed in deriving the new Pythagorean proof is characterized by a blend of innovative thinking and traditional mathematical techniques. The team of mathematicians responsible for this proof utilized a combination of algebraic manipulation, geometric construction, and logical reasoning to arrive at their conclusions. By integrating these diverse approaches, they were able to uncover novel insights that challenge conventional understandings of the theorem.
One of the key innovations of the new proof is its reliance on advanced algebraic techniques, which allow for a more nuanced exploration of geometric relationships. By leveraging these techniques, the team was able to identify previously overlooked patterns and connections, ultimately leading to a more comprehensive understanding of the theorem's implications.
In addition to algebraic methods, the new proof incorporates geometric constructions that provide visual evidence of its validity. These constructions not only serve to illustrate the proof's principles but also offer a tangible representation of the underlying mathematical concepts. By balancing algebraic rigor with geometric intuition, the new proof achieves a harmonious synthesis of traditional and modern mathematical approaches.
Implications for Modern Mathematics
The introduction of the new Pythagorean proof holds significant implications for the field of modern mathematics. By challenging established methodologies and offering fresh insights, this proof has the potential to influence a wide range of mathematical disciplines, from geometry to algebra and beyond. As scholars continue to explore its implications, this proof may serve as a catalyst for further innovation and discovery within the mathematical community.
One of the most notable implications of the new proof is its potential to inspire reevaluations of other fundamental mathematical principles. By demonstrating the value of innovative thinking and creative problem-solving, this proof encourages mathematicians to question conventional wisdom and explore alternative approaches to established concepts. In doing so, it fosters a spirit of curiosity and exploration that is essential for the advancement of mathematical knowledge.
Furthermore, the new proof's emphasis on interdisciplinary collaboration highlights the importance of integrating diverse perspectives and methodologies in the pursuit of mathematical discovery. By bringing together experts from various fields and backgrounds, this proof exemplifies the power of collaborative research and underscores the need for a holistic approach to understanding complex mathematical phenomena.
Applications in Science and Technology
The new Pythagorean proof extends beyond the realm of theoretical mathematics, offering potential applications in various scientific and technological fields. By enhancing our understanding of geometric relationships, this proof holds the potential to influence advancements in disciplines such as physics, engineering, and computer science, among others.
In physics, the new proof may provide novel insights into the study of spatial relationships and the behavior of physical systems. By offering a more comprehensive understanding of geometric principles, this proof could inform the development of new models and theories that enhance our understanding of the physical world.
In engineering, the new proof's emphasis on geometric construction and algebraic manipulation may inspire innovative approaches to design and problem-solving. By leveraging the insights gained from this proof, engineers may be able to develop more efficient and effective solutions to complex challenges, ultimately leading to advancements in technology and infrastructure.
In the field of computer science, the new proof's reliance on advanced algebraic techniques may inform the development of new algorithms and computational methods. By exploring the connections between geometric relationships and computational processes, this proof could pave the way for more sophisticated and efficient software applications.
Comparison with Traditional Proofs
The new Pythagorean proof represents a departure from traditional proofs, offering a fresh perspective on the geometric relationships that underpin the theorem. While traditional proofs have relied on established methodologies and techniques, the new proof introduces novel elements that challenge conventional understandings and invite further exploration.
One of the key distinctions between the new proof and traditional proofs is its emphasis on advanced algebraic techniques. By incorporating these techniques, the new proof offers a more nuanced exploration of geometric relationships, ultimately leading to a deeper understanding of the theorem's implications. This focus on algebraic manipulation sets the new proof apart from traditional geometric proofs, which have historically relied on visual representations and constructions.
Despite these differences, the new proof shares a common goal with traditional proofs: to demonstrate the validity of the Pythagorean theorem and enhance our understanding of its principles. By offering a fresh perspective and challenging established methodologies, the new proof contributes to the rich tapestry of mathematical knowledge and underscores the importance of innovation and exploration in the field of mathematics.
Educational Impact and Opportunities
The introduction of the new Pythagorean proof presents a unique opportunity for educators to engage students in the exploration of mathematical concepts and principles. By incorporating this proof into the curriculum, educators can inspire curiosity and foster a deeper understanding of geometric relationships, ultimately enriching the educational experience for students.
One of the key educational benefits of the new proof is its potential to encourage critical thinking and problem-solving skills. By challenging students to explore alternative approaches to established concepts, this proof fosters a spirit of curiosity and exploration that is essential for the development of mathematical proficiency. Furthermore, by emphasizing the importance of interdisciplinary collaboration, the new proof encourages students to appreciate the interconnectedness of various fields and the value of diverse perspectives.
In addition to its impact on mathematics education, the new proof offers opportunities for interdisciplinary learning and collaboration. By highlighting the connections between mathematics and other scientific disciplines, this proof encourages students to explore the broader implications of mathematical discovery and its potential applications in fields such as physics, engineering, and computer science.
Theoretical Implications and Future Research
The new Pythagorean proof holds significant theoretical implications, offering a fresh perspective on the geometric relationships that underpin the theorem. By challenging established methodologies and introducing novel elements, this proof invites further exploration and research into the fundamental principles of geometry and mathematics as a whole.
One of the key theoretical implications of the new proof is its potential to inspire reevaluations of other fundamental mathematical principles. By demonstrating the value of innovative thinking and creative problem-solving, this proof encourages mathematicians to question conventional wisdom and explore alternative approaches to established concepts. In doing so, it fosters a spirit of curiosity and exploration that is essential for the advancement of mathematical knowledge.
Furthermore, the new proof's emphasis on interdisciplinary collaboration highlights the importance of integrating diverse perspectives and methodologies in the pursuit of mathematical discovery. By bringing together experts from various fields and backgrounds, this proof exemplifies the power of collaborative research and underscores the need for a holistic approach to understanding complex mathematical phenomena.
Criticism and Controversies
As with any groundbreaking discovery, the new Pythagorean proof has sparked criticism and controversies within the mathematical community. While many scholars have embraced the proof's innovative approach and potential implications, others have raised concerns about its validity and the methodologies employed in its derivation.
One of the primary criticisms leveled against the new proof is its reliance on advanced algebraic techniques, which some mathematicians argue may obscure the geometric principles that underpin the theorem. By emphasizing algebraic manipulation over geometric construction, critics contend that the new proof may detract from the theorem's inherent elegance and simplicity.
Despite these criticisms, the new proof has garnered significant support from the mathematical community, with many scholars lauding its innovative approach and potential applications. As discussions and debates continue, the new proof is poised to become an integral part of the mathematical canon, inspiring future generations of mathematicians to explore the ever-evolving landscape of geometric theory.
Support from the Mathematical Community
The new Pythagorean proof has received widespread support from the mathematical community, with many scholars praising its innovative approach and potential implications. By challenging established methodologies and offering fresh insights into geometric relationships, this proof has captured the attention of mathematicians worldwide, sparking discussions and debates about its significance and potential applications.
One of the key factors contributing to the proof's support is its emphasis on interdisciplinary collaboration and the integration of diverse perspectives and methodologies. By bringing together experts from various fields and backgrounds, the new proof exemplifies the power of collaborative research and underscores the importance of a holistic approach to mathematical discovery.
As scholars continue to analyze and validate the new proof, it is poised to become an integral part of the mathematical canon, inspiring future generations of mathematicians to explore the ever-evolving landscape of geometric theory. By fostering a spirit of curiosity and exploration, the new proof serves as a catalyst for further innovation and discovery within the mathematical community.
Future Directions and Innovations
The introduction of the new Pythagorean proof marks a significant milestone in the ongoing exploration of mathematical principles, offering a fresh perspective on the geometric relationships that underpin the theorem. As scholars continue to analyze and validate the new proof, it holds the potential to inspire further innovation and discovery within the mathematical community.
One of the key areas of future research inspired by the new proof is the exploration of alternative approaches to established mathematical concepts. By challenging conventional wisdom and encouraging creative problem-solving, the new proof fosters a spirit of curiosity and exploration that is essential for the advancement of mathematical knowledge.
Additionally, the new proof's emphasis on interdisciplinary collaboration highlights the importance of integrating diverse perspectives and methodologies in the pursuit of mathematical discovery. By bringing together experts from various fields and backgrounds, the new proof exemplifies the power of collaborative research and underscores the need for a holistic approach to understanding complex mathematical phenomena.
Mathematical Philosophy and the New Proof
The new Pythagorean proof represents a significant departure from traditional proofs, offering a fresh perspective on the geometric relationships that underpin the theorem. By challenging established methodologies and introducing novel elements, this proof invites a reevaluation of mathematical philosophy and the principles that guide mathematical discovery.
One of the key philosophical implications of the new proof is its emphasis on innovative thinking and creative problem-solving. By demonstrating the value of questioning conventional wisdom and exploring alternative approaches to established concepts, the new proof encourages mathematicians to embrace a spirit of curiosity and exploration that is essential for the advancement of mathematical knowledge.
Furthermore, the new proof highlights the importance of interdisciplinary collaboration and the integration of diverse perspectives and methodologies. By bringing together experts from various fields and backgrounds, the new proof exemplifies the power of collaborative research and underscores the need for a holistic approach to understanding complex mathematical phenomena.
Global Perspectives on the New Proof
The new Pythagorean proof has captured the attention of mathematicians worldwide, sparking discussions and debates about its significance and potential applications. As scholars from diverse backgrounds and cultures explore the implications of the new proof, it offers a unique opportunity to foster global collaboration and exchange of ideas within the mathematical community.
One of the key factors contributing to the global interest in the new proof is its potential to inspire reevaluations of other fundamental mathematical principles. By challenging established methodologies and offering fresh insights, the new proof encourages mathematicians to question conventional wisdom and explore alternative approaches to established concepts, ultimately fostering a spirit of curiosity and exploration that transcends cultural and geographic boundaries.
Furthermore, the new proof's emphasis on interdisciplinary collaboration highlights the importance of integrating diverse perspectives and methodologies in the pursuit of mathematical discovery. By bringing together experts from various fields and backgrounds, the new proof exemplifies the power of collaborative research and underscores the need for a holistic approach to understanding complex mathematical phenomena.
Conclusion
The unveiling of the new Pythagorean proof represents a significant milestone in the ongoing exploration of mathematical principles, offering a fresh perspective on the geometric relationships that underpin the theorem. By challenging established methodologies and introducing novel elements, this proof invites further exploration and research into the fundamental principles of geometry and mathematics as a whole.
As scholars continue to analyze and validate the new proof, it holds the potential to inspire further innovation and discovery within the mathematical community. By fostering a spirit of curiosity and exploration, the new proof serves as a catalyst for the advancement of mathematical knowledge, ultimately enriching the educational experience for students and inspiring future generations of mathematicians.
The broader implications of the new proof extend beyond the realm of mathematics, offering potential applications in various scientific and technological fields. By enhancing our understanding of geometric relationships, this proof holds the potential to influence advancements in disciplines such as physics, engineering, and computer science, among others.
FAQs
1. What is the significance of the new Pythagorean proof?
The new Pythagorean proof represents a significant advancement in the exploration of geometric principles. By challenging traditional methodologies and offering fresh insights, it has the potential to inspire further innovation and discovery within the mathematical community.
2. How does the new proof differ from traditional proofs?
The new proof differs from traditional proofs by emphasizing advanced algebraic techniques and interdisciplinary collaboration. This approach offers a more nuanced exploration of geometric relationships, ultimately leading to a deeper understanding of the theorem's implications.
3. What are the potential applications of the new proof?
The new proof holds potential applications in various scientific and technological fields, including physics, engineering, and computer science. By enhancing our understanding of geometric relationships, it may inform the development of new models, theories, and algorithms.
4. What criticisms have been raised about the new proof?
Critics have raised concerns about the new proof's reliance on advanced algebraic techniques, arguing that it may detract from the theorem's inherent elegance and simplicity. Despite these criticisms, the proof has garnered significant support from the mathematical community.
5. How can the new proof impact mathematics education?
The new proof presents a unique opportunity for educators to engage students in the exploration of mathematical concepts and principles. By incorporating this proof into the curriculum, educators can inspire curiosity and foster a deeper understanding of geometric relationships.
6. What are the future directions for research inspired by the new proof?
The new proof holds the potential to inspire further research into alternative approaches to established mathematical concepts. By fostering a spirit of curiosity and exploration, it encourages mathematicians to explore the ever-evolving landscape of geometric theory.
For further reading on the Pythagorean theorem and its applications, you may visit this comprehensive resource on Wikipedia.
Spain National Team Euro 2012: A Remarkable Triumph
The Life And Journey Of Jennifer Garner's Oldest Daughter: A Comprehensive Insight
Ellie Bentley Go Fund Me: A Story Of Hope And Community Support

High Schoolers New Proof of the Pythagorean Theorem Using Trigonometry
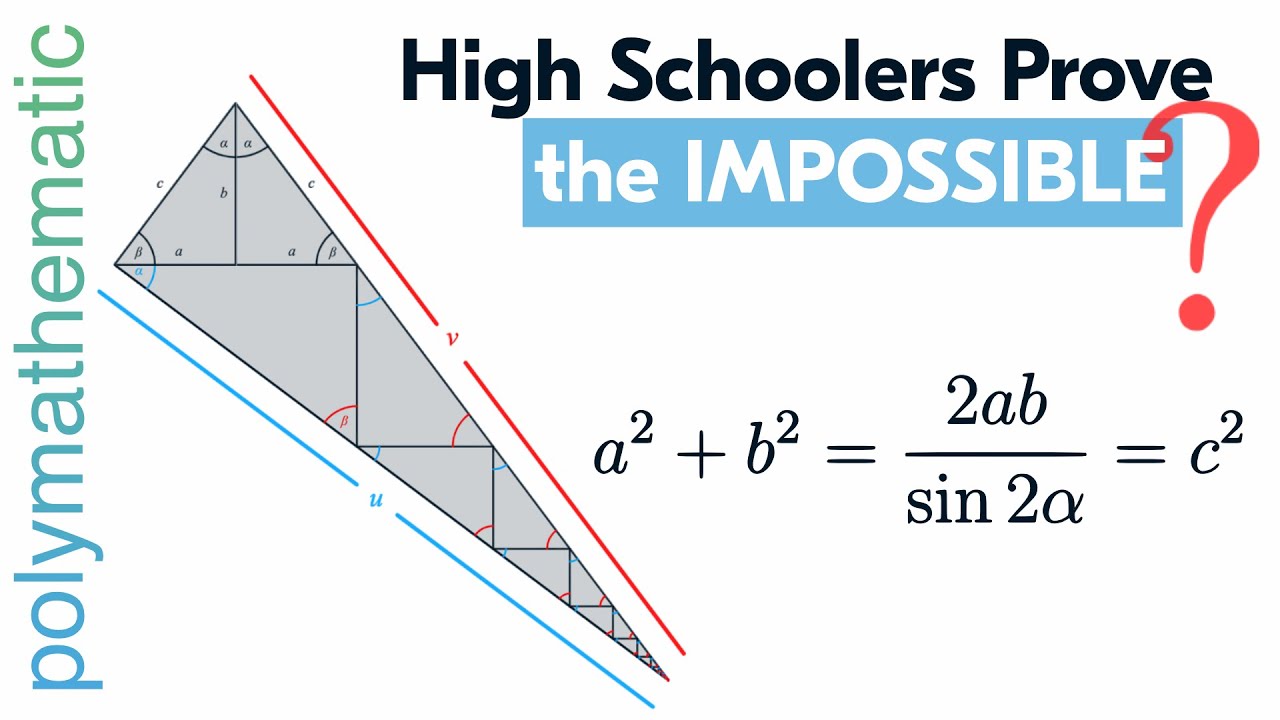
Pythagoras Would Be Proud High School Students' New Proof of the

The Metaphysics of the Pythagorean Theorem State University of New